❗이분 탐색
이분 탐색이란 정렬된 리스트 안에서 탐색 범위를 절반씩 줄여가며 원하는 값을 찾을 때까지 탐색하는 알고리즘이다
❗동작 방식
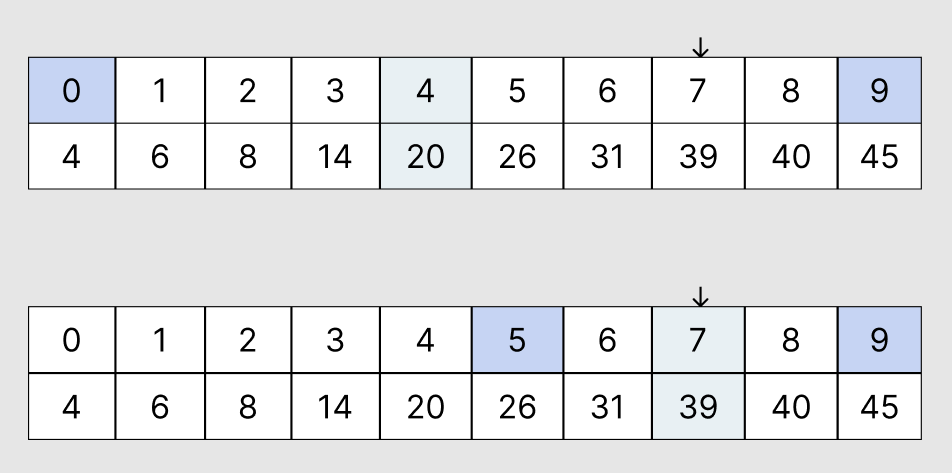
사전에 정렬된 리스트에서 39를 찾고자 한다.
1. start = 0, end = 9로 시작하여 두 값의 mid를 찾으면 인덱스 4가 된다.
data[4]가 가리키는 값이 20이므로 39보단 작기 때문에 start의 위치는 인덱스 4보다 1 더 큰 곳으로 변경한다.
2. start = 5, end = 9로 다시 탐색하면 mid는 인덱스 7이 된다.
data[7]이 가리키는 값은 타켓인 39와 동일하기 때문에 탐색이 종료된다.
이런 방식으로 target보다 현재 값이 작으면 start값을 변경하고, 크다면 end값을 변경한다.
❗파이썬 구현
이분 탐색은 반복문과 재귀 2가지 방식으로 구현할 수 있다.
1️⃣ 반복문
def binary_search(target, data):
start = 0
end = len(data) - 1
while start <= end:
mid = (start + end) // 2
if data[mid] == target:
return 1 # 존재
elif data[mid] < target:
start = mid + 1
else:
end = mid - 1
return 0 # 존재하지 않음파라미터로 찾고자하는 값과 정련된 리스트를 받고, 초기의 start와 end를 할당 후 while을 통해 탐색하고 있다.
2️⃣재귀
def binary_search(target, data, start, end):
if start > end:
return 0 # 존재하지 않음
mid = (start + end) // 2
if data[mid] == target:
return 1 # 존재
elif data[mid] < target:
start = mid + 1
else:
end = mid - 1
return binary_search(target, data, start, end)파라미터로 찾고자하는 값과 정련된 리스트를 받고, 해당 시점에서의 start와 end도 같이 받고 있다.
그래서 if문을 통해 start와 end 지점을 변경 후 return으로 다시 재귀 호출한다.
❗참고 문제
https://www.acmicpc.net/problem/1920
https://radiant515.tistory.com/509
[Baekjoon] 백준 1920 수 찾기 Python
https://www.acmicpc.net/problem/1920import sysn = sys.stdin.readline()data = list(map(int, sys.stdin.readline().split(" ")))m = sys.stdin.readline()find_data = list(map(int, sys.stdin.readline().split(" ")))data.sort()# 반복문def binary_search(target, d
radiant515.tistory.com
'🔻Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] Recursion 이론 + 예제 (0) | 2024.09.04 |
|---|---|
| [Algorithm] 우선순위 큐 이론 + heapq 사용법 (0) | 2024.08.09 |
| [Algorithm] 백트래킹(+순열, 조합) 이론 + 구현 (0) | 2024.07.29 |
| [Algorithm] BFS 이론 + 구현 (0) | 2024.05.03 |
| [Algorithm] DFS 이론 + 구현 (0) | 2024.05.03 |
